
STAD CC 533 Testing of Hypotheses
This course is offered for III-semester MSc Applied Statistics and Data Analytics students of the Department of Statistics.
Testing of Hypotheses is an important core area in Statistics. Imparting knowledge through this course makes the students competent in pursuing for research in this area as well as for carrying out various statistical tests.

STA CC 533 Testing of Hypotheses
This course is offered for III-semester MSc Statistics students of the Department of Statistics.
Testing of Hypotheses is an important core area in Statistics. Imparting knowledge through this course makes the students competent in pursuing for research in this area as well as for carrying out various statistical tests.
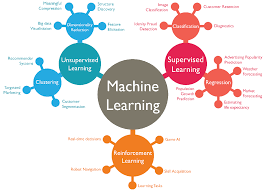
MACHINE LEARNING
SEMESTER : II
COURSE CODE : STAD-CC-521
COURSE TITLE : MACHINE LEARNING
CREDITS :4
COURSE OUTCOMES:
On completion of this course, students should be able to:
CO1 : Analyze the data and understand the insights from it.
CO2: A clear understanding of machine learning algorithms and applications.
CO3: Apply various ML techniques as per the requirements
CO4: Calculate the maximum likelihood estimation
CO5: Differenciate bias and variance estimation
CO6: To calculate the number of clusters for clustering algorithms
CO7: The full derivation of forward and backward propagation in neural network

DATA ANALYTICS USING R
COURSE OUTCOMES
C01.Define the basic concepts of R software and R packages
C02.Describe various concepts required for developing the R Language
C03.Build our own new functions in R
C04.Illustrate different R-Graphics facilities
C05.Perform programming of different statistical methods and procedures
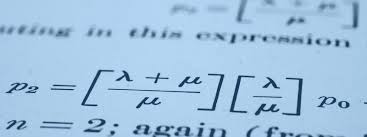
STATISTICAL MATHEMATICS
The course is given as a prerequisite to the papers such as Distribution Theory,
Multivariate Analysis, Probability Theory, Estimation, Testing of Hypothesis, Non-Parametric Methods, Stochastic Process, Advanced Probability Theory (Elective), Real Analysis and Econometric Methods (Elective), Bayesian Inference (Elective), Order Statistics (Elective), Actuarial Statistics (Elective) and Operations Research (O.R) (Elective).
Attainment of analytical skills to analyze problems in Statistics is highly
essential. The course will consist of lectures and related activities that will help in developing
good understanding of basic concepts in Statistical Mathematics. STAD-C- 411: Statistical
Mathematics is designed in such a manner to impart knowledge on Measure Theory, Real
Analysis, Theory of Integrals, Vector Spaces and Matrix Theory and Quadratic Forms.

OPERATIONS RESEARCH
To equip the students with knowledge in Statistics to become efficient managers.
This course is meant to give an introduction to various types of optimization problems including linear and nonlinear programming problems,that mainly arise in management science. Students with deep knowledge in Statistics can excel in the field of management with their knowledge in Operations Research course offered in this semester.

MEASURE THEORY
The aim of this course is to impart the students the knowledge of measure theory to
treat any problem in Mathematical Statistics in a measure theoretic approach so that the
results developed in Measure Theory can be adopted as such in the statistical problem of their
curriculum.
The course will consist of lectures and related activities that will help in
developing good understanding of basic concepts in Measure Theory, which serves as a
prerequisite
to any course in Mathematical Statistics such as Probability Theory, Distribution
Theory, Stochastic Process Estimation, Testing of Hypothesis, Non-Parametric Methods,
Bayesian Inference (Elective), Advanced Probability Theory (Elective) and Order Statistics
(Elective).
Statistical Computing
For applications of statistical methods to various problems arising in real life situation the presently available statistical softwares are used. But there are situations in which software application alone may not solve the problem and sometimes the students have to deal with statistical application in the absence of proper software. Hence this course is designed in such a way that the students attain a caliber of writing computer programs to statistical problem by their own way.

ELEMENTS OF PROBABILITY THEORY
This is a two credit course offering as a Generic Course during second semester of PG programmes from Department of Statistics, University of Kerala. Even though it is offered as an Extra Departmental Elective Course, its syllabus is quite heavy and those who are really interested to study Probability Theoretic concepts are welcome to join. Probability Theory provides basement to almost all scientific theories. As such the topic is quite abstract in nature, but interesting. The syllabus is divided into five modules.

PROBABILITY THEORY
On completion of the course, students should be able to:
CO1. Identify a probability measure and explain its properties
CO2. Solve problems based on various properties of a probability measure
CO3. Apply the concepts of Baye's theorem and solve related problems
CO4. Distinguish between a discrete and continuous type random variables and illustrate with
examples
CO5. Verify the properties of important functions of random variables
CO6. Calculate the expectation and moments of random variables and random vectors
CO7. Identify the applications of various moment inequalities
CO8. Explain the concept of convergence and check for the of convergence of a given sequences
of random variables.
CO9. Find the expressions for the characteristic function of a random variable and verify its
properties
C10. Apply the various laws of large numbers to sequences of random variables.
STOCHASTIC PROCESSES
Describe and exemplify concepts of Stochastic processes, time space and state space, classification of stochastic processes based on the nature of time space and state space, Classical stochastic processes like processes with stationary independent increments, Markov process, renewal process, martingales, Wiener process, Gaussian process;
Explain Markov chains: Definition, transition probability matrix, n-step transition Probability and Chapman-Kolmogorov equation;
Calculate n-step transition probabilities;
Classify states of a finite Markov chain;
Describe periodicity and ergodicity of chains;
Describe limiting behaviour of n-step transition probabilities;
Obtain the stationary distribution of a Markov chain;
Describe random walks & gambler’s ruin problem;
Explain and exemplify continuous time Markov chain, Poisson process, pure birth process, birth and death processes, compound Poisson process, Markov Process with discrete states;
Distinguish between strict and weak (covariance or wide sense) stationarity;
Explain and exemplify renewal processes, renewal equation;
Describe and apply renewal theorem;
Describe Branching processes, offspring distribution, extinction probabilities.